15 February, 2020 (Ogle, CHANCE, SAM)

Kiona Ogle & Jarrett J. Barber (2016) Plant and Ecosystem Memory, CHANCE, 29:2, 16-22, DOI: 10.1080/09332480.2016.1181961

• Why did I read this paper?

It is often easier to get knowledge (i.e., model, concept, equation, and so forth) not from the original descriptive paper, but from other papers using the knowledge because they introduce the knowledge after masticating it, not as it is.

This paper masticates the stochastic antecedent modelling (SAM) framework for beginners. This study describes what SAM does and how SAM does it, and why SAM does it with a simple example and without complicated equations. Whereas, the original paper (Ogle et al., 2015¹) provides in-depth explanation about the SAM, but the mathematical expressions cover here and there, making readers terrified even though the two studies exemplified the same case.

1. Antecedent (or memory) effect

Antecedent effect (the effect of the past on current and future plant and ecosystem functioning) is the key concept gives birth to the SAM. We can see many cases of antecedent effect. For example, in the NBA, a ball handler can break the defender’s ankle because the offender’s cross-over a few moment ago affects the defender’s movement later. By the same token, in a soccer game, the goal keeper can dive into the opposite direction when the ball is refracted because the time when the shooting was made affected the goal keeper, but the time when the ball is refracted has not done yet. In the nature, there are also many processes influenced by conditions in the past (such as photosynthesis, transpiration, leaf flushing, growth, and so forth), but the leverage differs by the timing and variables. Therefore, it is the key to estimate the leverages for each time in the past and variables.

2. SAM framework

SAM estimates the leverage (the authors used the term “weights") by the Bayesian approach. The theoretical details and ways to implement this approach are not described in this paper.

3. Figure 1. Importance of accounting the memory (or weights)

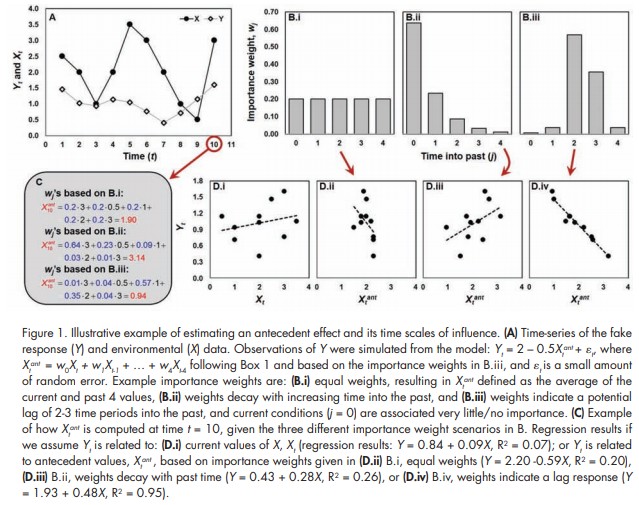
The authors provides a toy data set which consists of X and Y (simulated from the X). When applying the classical regression approach (D.i), it seems that there is only trivial relationships between X and Y (R² = 0.07). However, when the memory effect is considered, stronger relationships appear (D.ii ~ D.iv), and the score differs by how the weights for each time assigned (B.i ~ B.iii).

4. Figure 4. Interpreting the nature’ memory effect from weight estimates

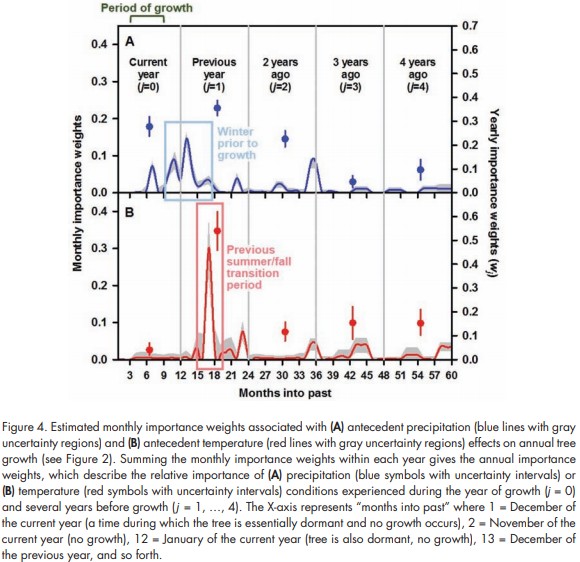
The authors exemplifies a tree-ring growth (G) analysis explained by temperature (T) and precipitation (P) data sets. Monthly weights of T and P were estimated by the SAM and annual weights were given as the sum of 12 month weights of the year. Accorting to the results, P during the winther prior to the growth (probably implies the importance of the snowmelt) and T during summer-autumn transition period of the year before the growth. This shows that G has a longer-term memory for T than for P. As the instance shows, a researcher can verify the existing assumption or draw unexpected implication by weight estimates of SAM.

5. What’s next?

• How to implement** the SAM framework?: Professor Ogle usually uses R packages.

• How does Bayesian determine the weights?

• For what do I apply the SAM for my research?

  Possibly, I can apply the SAM for two studies for quantifying the lagged response (or memory effect):

  1. lagged response of fuel moisture content after the end of precipitation

  2. mismatched responses between transpiration (Granier sensor) and net ecosystem exchange (Eddy)